As a kid I fantasized about how great it would be to have a map on which you could see where you are, like the Marauders Map of Harry Potter. Who could have thought that a couple of years later there would be a technology that makes it possible, a technology so brilliant that it even takes into account Einsteins’ special theory of relativity.
Since my first GPS I am always looking for the most accurate GPS for logging my sports and hiking trips. I started in 2007 with the Garmin GPSMAP 60csx, but it was quite bulky for running (I had to keep it in hand). I therefore switched to the relatively unknown I-gotU devices. They were succeeded by the TomTom weareables (Adventurer) and they seemed pretty accurate (I still use them for open water swimming, attached to my buoy). Since they were discontinued I switched to Garmin. On my bike I have used the Edge 810, Edge 830 and am currently using the Edge 1040. For running and swimming the Fenix 7 and for hiking I recently bought the GPSMAP 67. The latter 3 are currently the top-of-the-bill consumer models from Garmin that use multiple satellite systems.
I’ve been using the Fenix 7 and Edge 1040 for quite some time now and they are giving good results and good agreement if I use them both (and I often do). I expected the GPSMAP67 to perform at least as good as them, if not better, since it has the same GPS chip, but a better antenna. So I took all three of them on a MTB trip through the forest. Auch! The result of the GPSMAP 67 was a bit disappointing: it’s track deviated from the Fenix 7 and Edge 1040 tracks. Though the Fenix and Edge are in good agreement with each other throughout the entire trip, the GPSMAP 67 showed deviations. And yes, two against one…
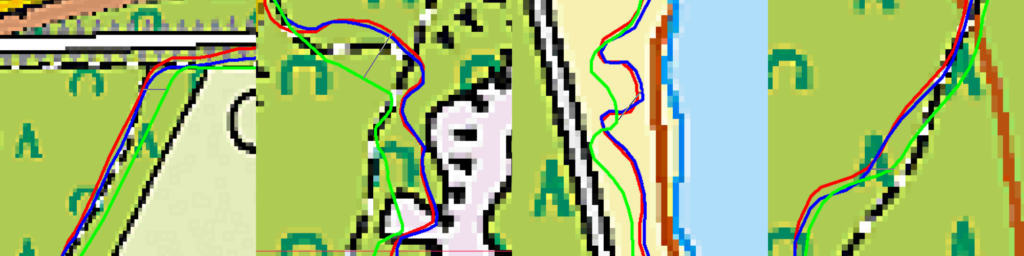
Reason to put them on the test bench for a more thorough examination…
Disclaimer: yes, I am a GPS weirdo 🤪and I go to the last cm. If you think: ‘Man, what are you fuzzing about?‘, stop reading here.
Important notice: during testing I found a serious issue on the GPSMAP 67 on which I reported in another post. Due to this issue the GPSMAP67 is unreliable because it might show your location with a large error. I reported it to Garmin Support but they don’t take it seriously and just refer to their FAQ.
The contestants
Apart from the Garmins I put the TomTom Adventurer also to the test, since I have good experience with it, though it is outdated.

| Device | Chipset | Antenna | Form factor | Color in graphs |
| TomTom Adventurer | Sirfstar V | ? | Watch | Magenta |
| Garmin Fenix 7 | Airoha AG3335MN | ? | Watch | Blue |
| Garmin Edge 1040 | Airoha AG3335M | ? | Bike computer | Red |
| Garmin GPSMAP 67 | Airoha AG3335M | Quad Helix | Handheld | Green |
The Garmin devices were used in multi-band, GNSS mode, which means they use 4 satellite systems: GPS, Glonass, Beidou and Gallileo. TomTom just uses GPS. Recording mode was interval, one record per second. No clipping to roads. Autostart and Autopause off. Recording only during activity. No power saving (no ‘expedition mode’ etc).
What we want to know
The goal of this research is to estimate how accurate the device log position:
- track logging during movement
- position indication when stationary (e.g. during Geocaching)
- manually logging a waypoint
We want to know on the average what error (distance between indicated location and actual location), expressed in meter, we might expect.
What we expect
Garmin expresses what we might expect on its FAQ:
GPS drift, in the most practical sense, is the difference between your actual location and the location recorded by a GPS receiver. Since consumer-grade GPS receivers (such as the ones Garmin makes) are not 100% accurate, this can cause a difference between your actual location and your recorded location.
The GPS location accuracy of Garmin outdoor watches is around 3 meters (10 feet), 95% of the time. This means, at any given time, your watch will save your location within 3 meters of your actual location. If your watch is recording a GPS location every second and you do not pause an activity while standing still, your watch can record up to 180 meters (590 ft) in just 1 minute. When in an area with degraded GPS signals, your watch can record even more distance while stopped. The distance recorded while standing still is a representation of GPS Drift.
Yep, that makes sense: your position always comes with an error. Devices usually indicate cumulative distance. And yes, if you’re standing still this distance may increase due to this error. But we are not interested in this.
So basically for wearables the position indicated is within 3 meters from the actual location 95% of the time. 5% it may be further off (assuming a normal distribution: 95% fall within 2σ=3m, σ=1.5 m). The GPSMAP 67 indicates the error as 1.8 m under good conditions (in fact we don’t know the definition of this 1.8 m. Is it σ? Is it 2σ?). So we expect the indicated position to be within this distance from the actual location most of the time. Of course, the error is highly affected by the conditions under which the device is used (buildings around, under trees, weather, bad hair days, …).
Accuracy versus precision
First a word about what we measure with a GPS. A GPS unit measures its location on earth (coordinate) based on receiving satellite signals. It knows the satellite location and measures how long the signal took to reach the GPS. It used triangulation to estimate its location. The more satellites it ‘sees’, the more accurate the location. I guess it applies all kind of dark magic like filtering and smoothing to get an accurate value. However, as with all measurements an error is associated with the location. If we measure the location multiple times on the same location, the measurement value varies.
We discern Accuracy and Precision. Accuracy is a measure of how well the measurements coincide with the actual location. Precision is a measure for the repeatability: the smaller the error, the higher the precision. Next picture shows that Accuracy and Precision do not need to coincide.
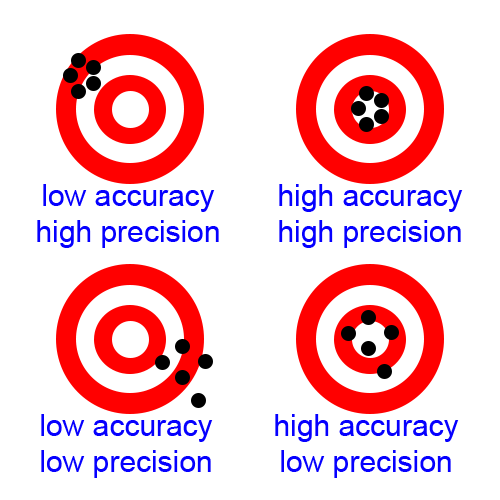
CPE or Circular Error Probable is a measure for precision. It defines a circle around the aimpoint in which half of the measurements fall. So the other half falls outside. in the graphs below we indicate this circle.
Error
Since we want to measure precision and accuracy we have to take into account all sources of errors and the errors they generate that influence the result
References
We use a Rijksdriehoeksmeting reference point. The actual measurement error we do not know. We assume ~1cm, which is the accuracy of current measurement equipment.
We use a 4 Mile reference distance, normally used for sports. We do not know the error but assume ~1 meter.
Calculations
We convert WGS84 lat lon coordinates (EPSG:4326) from the GPS to Dutch Grid (RDNew coordinates, EPSG:28992) using MapDatumConvert. This results in an easting and northing in meters. The calculation error is < 1 cm.
Projection error is the error due to the stereographic projection. In a circle with radius 122 km around Amersfoort this error is 0. In the rest of the Netherlands it is less 0.02% (scale at Amersfoort -0.01%, borders of NL +0.02%). Since we were close to this 122 km circle, we neglect this error.
Distance calculation is an interesting topic. I found an error between the Haversine method (on lat, lon) and RD method of ~0.1%. We use Pythagoras rule with the RD coordinates. I believe in the Netherlands this is the most accurate method.
Precision measurement
Stationary placement
The first test that was performed was a precision test. The devices were left in the garden on the ground. Clear view of the sky, which was clouded and foggy. The first test lasted 2 hours. WGS84 latitude and longitude were measured. I converted it to RDNew coordinates (which is the Dutch grid, EPSG:28992). This map datum expresses coordinates as easting and northing in meters. I subtracted the average value. This resulted in scatter plots.
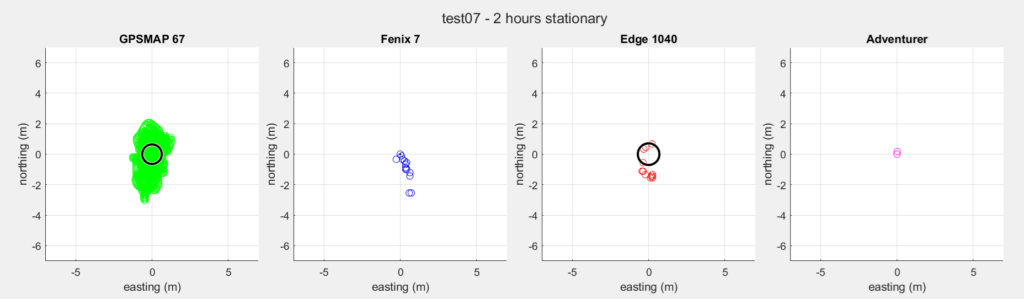
| GPSMAP 67 | Fenix 7 | Edge 1040 | Adventurer | |
| Measurements | 7690 | 7661 | 7659 | 7657 |
| Time | 2h 8m 14s | 2h 7m 40s | 2h 7m 38s | 2h 7m 36s |
| Average distance | 0.76 m | 0.01 m | 0.88 m | 0.00 m |
| Max. distance | 3.09 m | 2.64 m | 1.57 m | 0.17 m |
| CPE | 0.64 m | 0.00 m | 0.71 m | 0.00 m |
The GPSMAP 67 shows what we might expect: a nice distribution around a center value. The other show only a few values which repeat over and over again. The latter I do not trust. This suggests some kind of dead-band filtering or hysteresis, which means a measured value must be significantly different from the previous in order for it to be recorded as a new value. This makes the comparison unfair.
In a second run the Garmin devices were left outside for 12 hours. The TomTom was excluded because its battery wouldn’t last.
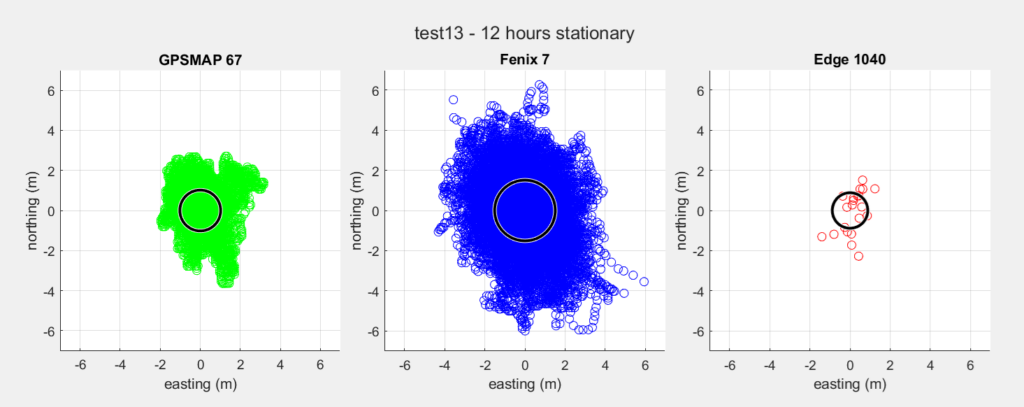
| GPSMAP 67 | Fenix 7 | Edge 1040 | |
| Measurements | 44284 | 44247 | 44225 |
| Time | 12h 18m 19s | 12h 17m 26s | 12h 17m 7s |
| Average distance | 1.13 m | 1.59 m | 1.15 m |
| Max distance | 3.91 m | 6.91 m | 2.31 m |
| CPE | 1.02 m | 1.51 m | 0.88 m |
Now we see a more realistic pattern for the Fenix 7, whereas the Edge 1040 still indicates only a few possible values. On a second 12 hours measurement, the Fenix was back to a few values though. So for a comparison this is not really usable.
For the GPSMAP 67 we peformed a experiment to estimate the effect of antenna alignment. Next charts show the GPSMAP 67, one hour vertically, one hour lying horizontally on its back.
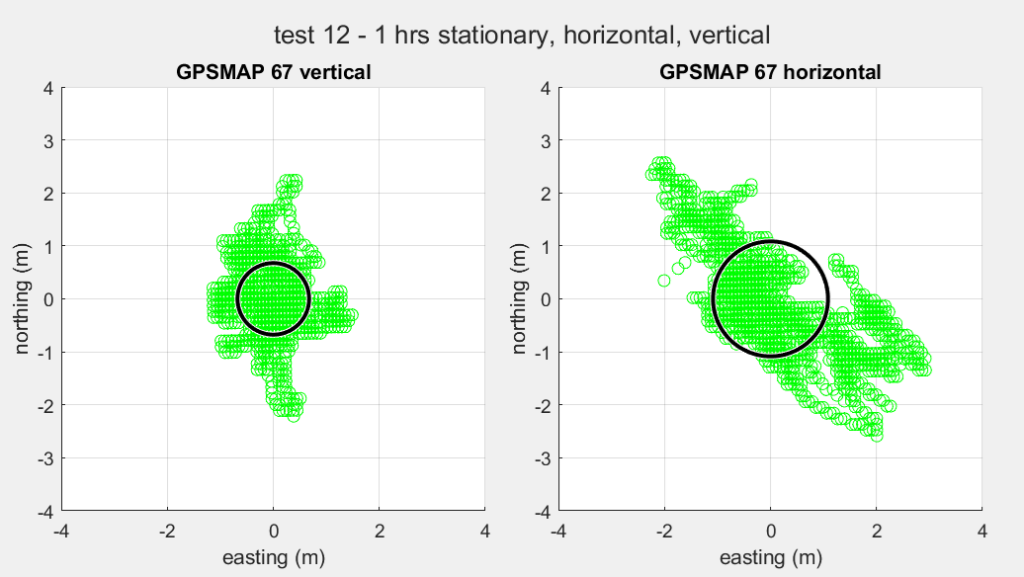
| GPSMAP 67, vertical | GPSMAP 67, horizontal | |
| Measurements | 4227 | 4128 |
| Time | 1h 10m 28s | 1h 8m 47s |
| Average error | 0.75 m | 1.25 m |
| Maximum error | 2.28 m | 3.33 m |
| CPE | 0.68 m | 1.08 m |
As is obvious, keeping the device upright gives a more precise reading.
Two anomalies were observed with the GPSMAP 67. Both are shown in the picture below:
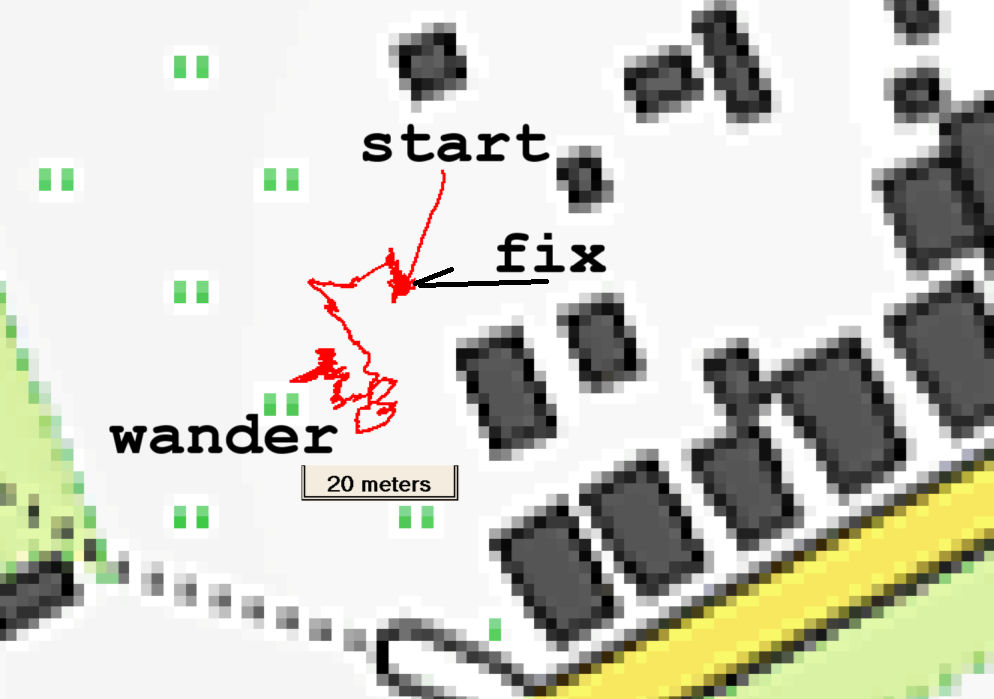
- Start error
Sometimes when starting the log the coordinate is meters off. However the coordinate converges within a few minutes to the ‘real’ location. In the example the error persisted for 340 seconds before converging. It may be the residue of next issue: - Wandering off
Sometimes the measured value starts wandering off. The distance error gets quite high. An error of 152 m has been observed. It doesn’t seem to converge to the ‘real’ location again. Only switching the device off and on again immediately solves the problem.
The problem seems to occur more in horizontal position. This problem has been described in another post.
So we conclude following:
* The GPSMAP 67 shows an average precision error of 0.8 m over 2 hours, 1.1 m over 12 hours
* Because of some dead-band filtering mechanism we cannot conclude about the other devices
* The GPSMAP 67 is more precise in vertical position (error 0.8 m) than in horizontal position (1.2 m) when we measure for one hour.
* Under less ideal conditions the GPSMAP 67 shows abnormal behaviour in stationary situation
Walking a line
So in order to get a fair comparison we need to move. Next precision measurement has been made with all 4 GPSses by walking a straight road of about 900 m. GPS coordinates were converted to RDNew (the Dutch grid expressing coordinates in ‘easting’ and ‘northing’, in meters). A fit was made for each dataset using linear least squares method (minimizing the orthogonal distances of the point to the line). Next, the shortest distance of each point with respect to this fitted line was calculated.
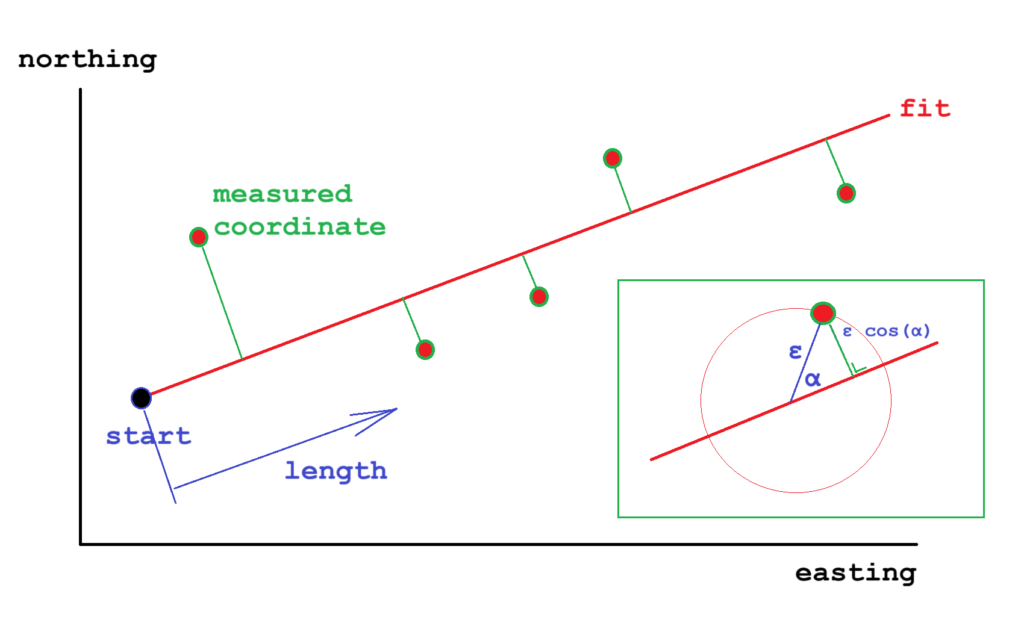
Next charts plot this shortest distance to the line (error) as function of the length from the start coordinate. I estimate the position of the GPS with respect to the road to vary +/- 0.1 m. Since there is no correlation between the charts, it can be concluded that the error is mainly measurement error and walking deviation and not error due to bends in the road. In other words: the road really is straight.

If the absolute location error in m is ε than it is clear that in this way we actually measure ε cos(α) which is the shortest distance to the fit, as is shown in the inset. Assuming alpha is randomly distributed, and the average of cos(α) is √2. Next table therefore shows the average of ε, which is the average of the absolute value of the measured distance times √2.
| GPSMAP 67 | Fenix 7 | Edge 1040 | Adventurer | |
| Average error ε (m) | 0.26 | 0.41 | 0.37 | 0.74 |
The measurement was repeated for GPSMAP67 and Fenix 7, in which the distance was covered twice, to and fro. Both are plotted in the same graph.
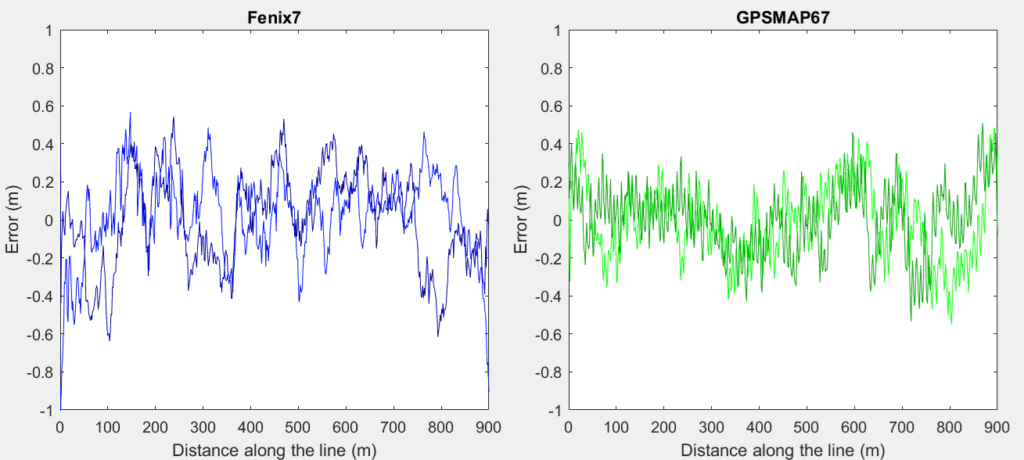
| GPSMAP 67 | Fenix 7 | |
| Average error ε (m) | 0.24 0.20 | 0.27 0.30 |
The error found this way is remarkably low. The time measured was about 11 minutes. ~650 coordinates were recorded. Maybe during such a short time the error doesn’t vary much. Alternatively, some filtering may have been applied.
The GPSMAP 67 graphs shows remarkable wave structure. Perhaps this was due to the fact that the device was hanging from a rope on the shoulder and was swinging a little with every step. Since it is not to be expected that this swinging has effect on satellite reception and therefore on the GPS coordinate, it suggests that somehow the device also takes the acceleration sensor or/and electronic compass signals into account.
This swinging was not present in the first measurement, which can be explained by the fact that the GPSMAP 67 was stationary in a breast pocket and not swinging.
We conclude following:
* The Garmin devices show a low precision error of 0.2-0.4 m, when moving along a straight line
* The TomTom Adventure shows a larger precision error of 0.7 m
* The GPSMAP 67 shows some indication that it might also use acceleration sensors for positioning
Moving
I took the 4 contestants out on a bike trip and cycled the same lap 14 times. I made sure I followed the same location on the road over and over again, so I estimate the real positioning error about +/- 0.2 m.
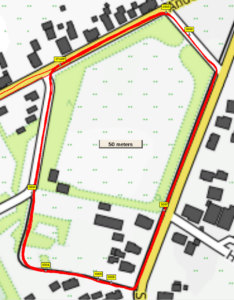

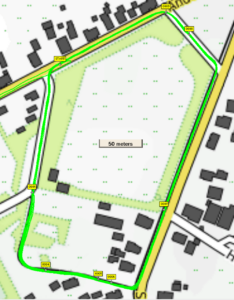
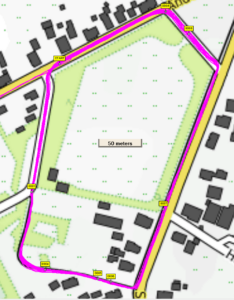
The ‘Start’ point was the coordinate that appeared in each lap twice, as start and as end. Based on the measurements the distance of each lap was calculated by first converting to RDNew coordinates (easting, northing) and using Pythagoras. Of course measurements did not coincide exactly with the start point. Since the record interval was 1 second, the closest measurement to ‘Start’ was within +/- 0.5 second from ‘Start’. At a speed of 6 m/s, this would introduce an error of average 1.5 m at the start and at the end. The total error on the lap distance would by sqrt(2*1.5^2)= 2.1 m on average (which is substantial). Therefore we interpolated and looked for the point on the track (in between 2 measurements) that was really closest to ‘Start’. Average lap distance and standard deviation were calculated and are shown in next diagram. The circle radius is one standard deviation. The y axis indicates the mean lap distance.
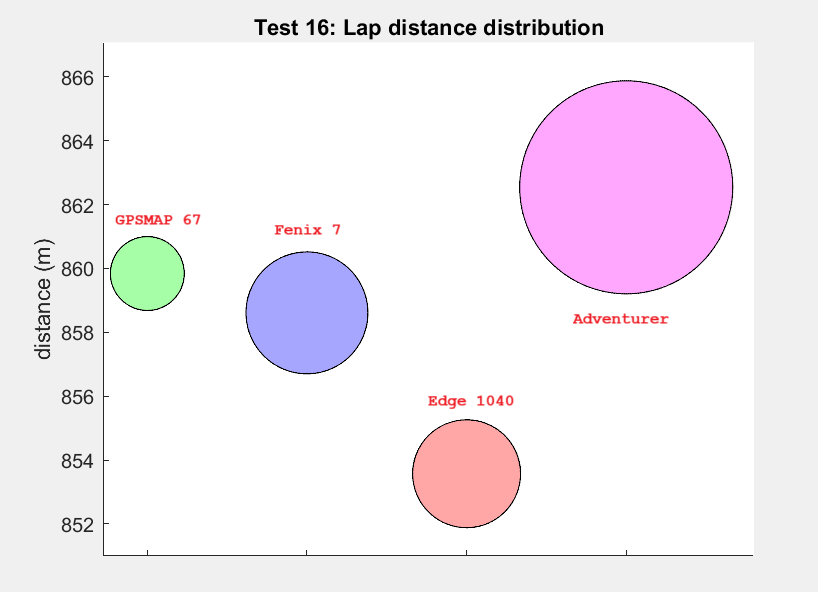
| Average Lap distance (m) | Standard Deviation (m) | |
| GPSMAP 67 | 859.8 | 1.2 (0.13%) |
| Fenix 7 | 858.6 | 1.9 (0.22%) |
| Edge 1040 | 853.6 | 1.7 (0.20%) |
| Adventurer | 862.5 | 3.3 (0.39%) |
So results are pretty precise. The results of the Garmins are within 1% with respect to each other.
Accuracy Measurement
Distance measurement
First accuracy comparison was made by cycling a know distance of 4 Mile (6437.376 m). This distance is indicated on the cycle path by a start and an end marker. I logged this markers with a waypoint. Unfortunately I do not know the accuracy in the distance of this track.
I cycled the track 4 times. Fenix 7 on left wrist, Adventurer on right wrist, Edge 1040 on steering rod, GPSMAP 67 in breast pocket (1st two laps) and on shoulder (last two laps). Good sky view, some trees but no leaves. Blue sky.
I did this experiment also in 2017 in which the Adventurer was tested. Then I did six laps on the same track. However, the markers no the road have been replaced since then. Also the I changed the calculation method from haversine (2017) to RDNew/Pythagoras (now). To compare the distances I processed the 2017 data with respect of the markers and calculation method of today.
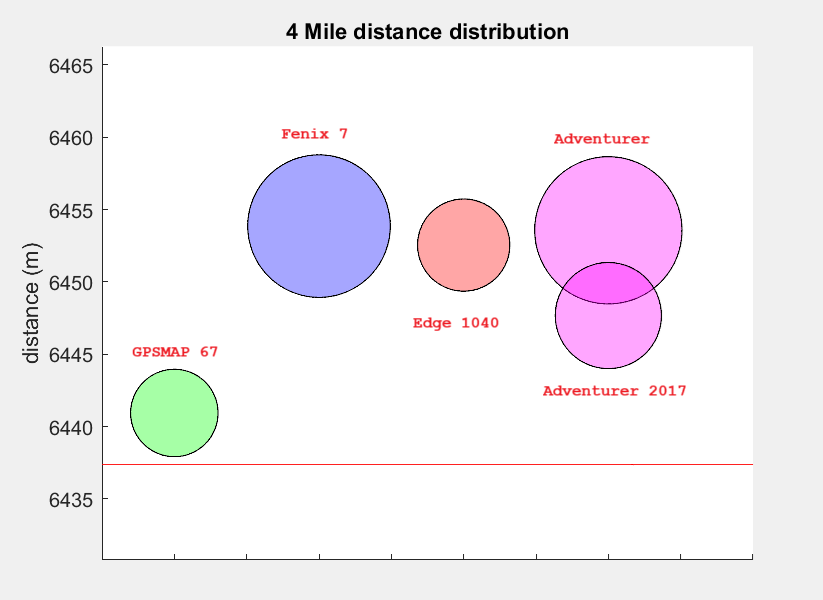
| Average lap distance (m) | Accuracy | Standard Deviation (m) | |
| GPSMAP 67 | 6440.9 | +0.05% | 3.0 |
| Fenix 7 | 6453.9 | +0.26% | 4.9 |
| Edge 1040 | 6452.6 | +0.24% | 3.2 |
| Adventurer | 6453.6 | +0.25% | 5.1 |
| Adventurer – 2017 (6 laps) | 6447.7 | +0.16% | 3.7 |
The red line in the graph represents the 4 Mile distance. First of all, all the GPSses perfomed quite well with deviations of 0.3% and below with respect to the actual 4 mile distance! The GPSMAP 67 shows the most precise value with a standard deviation of 3 m. It also appears the most accurate, but since we do not know the error in actual track, we cannot conclude for sure.
The GPSMAP 67 appears to be on the low side comparing to the other contentants. Looking at the tracks, the GPSMAP 67 usually coincides with the Edge 1040 and Fenix 7 though on certain points it shows a consistently different behaviour.
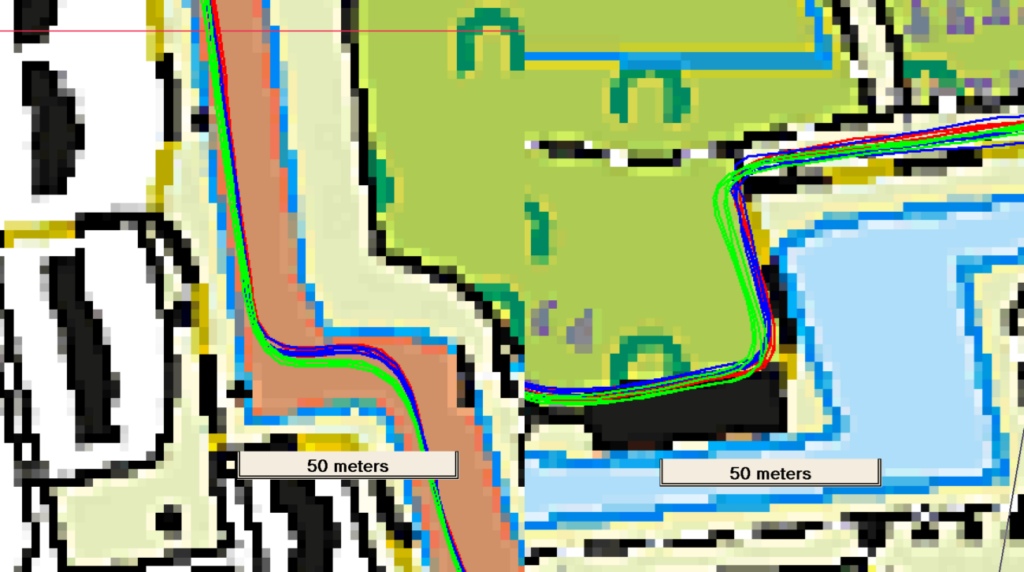
Especially on the left hand side picture it seems so smooth the corners a bit more, accounting for the missing meters.
We conclude following:
* The GPSMAP 67 shows the best precision in both distance measurements
* In the 4 mile test all tested devices show an accurate distance under clear sky conditions. The GPSMAP 67 seems most accurate. But to be conclusive on this we need to know the error in the reference distance, which in fact we do not.
Accuracy in coordinate position
To test the accuracy (i.e. how well does the indicated coordinate coincide with the real coordinate) a point was used with known coordinate, reference point 120324-11 in the Dutch Rijksdriehoekscoordinaten system (available online as RDInfo dataset). Its RDNew coordinate is [249021.985, 560371.895]. Unfortunately the error is not published but I assume it must be in the order of 1 cm which we can neglect. Conditions were ideal as is visible in the photo below of the reference point: unobstructed clear blue sky.
The procedure followed was, after starting the GPS and waiting for a while:
- Log a waypoint on all GPSses in quick succession, at the reference point
(Order: Adventurer, Edge 1040, GPSMAP 67, Fenix 7) - Walk 20-100 m away from the reference point in one of a few ‘random’ directions
- Walk back to the reference point
- Log next waypoint
In this way we try to circumvent the dead-band effect found in earlier measurements and try to obtain independent measurements. Stated otherwise: we simulate a real life situation in which we follow a track and log a waypoint.
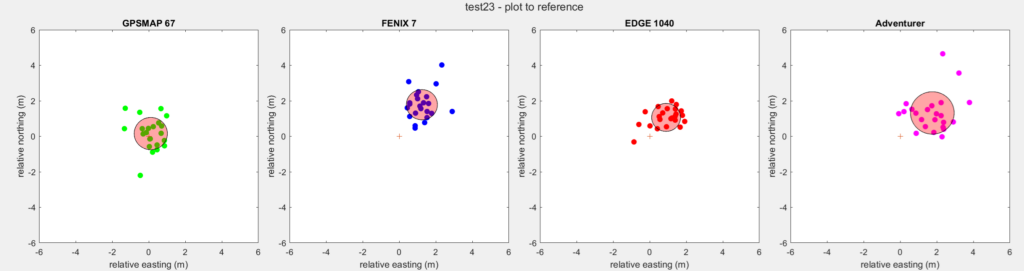
The results of the first test on 02-02-2025 are shown in the graph and table below. The center of the graph (+ marker) at (0,0) is the reference point, the dots show the actual measured positions (16 points) with respect to this reference point (the reference has been subtracted from the position). The large circle is placed at the average measured coordinate, its radius is equal to the average error with respect to this average coordinate (hence, it indicates the precision).
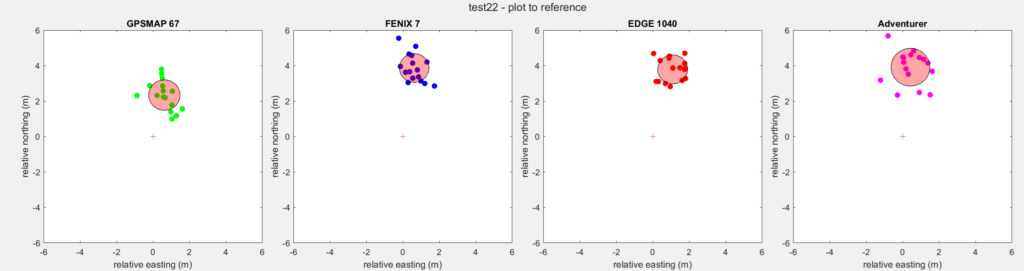
| GPSMAP 67 | Fenix 7 | Edge 1040 | Adventurer | |
| Measurements | 15 | 15 | 15 | 15 |
| Measurement time | 1h | 1h | 1h | 1h |
| Average accuracy error (m) | 2.5 | 4.0 | 4.0 | 4.0 |
| Average precision error (m) | 0.9 | 0.8 | 0.8 | 1.1 |
What appears is that all GPSses measure a location NNE of the true position (systematic error). The GPSMAP 67 appears to be most accurate, with an average accuracy error of 2.5 m, whereas the other three indicate 4.0 wrong.
To investigate the systematic error, the experiment was repeated a day later (03-02-2025) and 3 days later (05-02-2025).
| GPSMAP 67 | Fenix 7 | Edge 1040 | Adventurer | |
| Measurements | 23 | 23 | 23 | 23 |
| Measurement time | 40′ | 40′ | 40′ | 40′ |
| Average accuracy error (m) | 0.9 | 2.3 | 1.6 | 2.4 |
| Average precision error (m) | 0.9 | 0.9 | 0.8 | 1.2 |
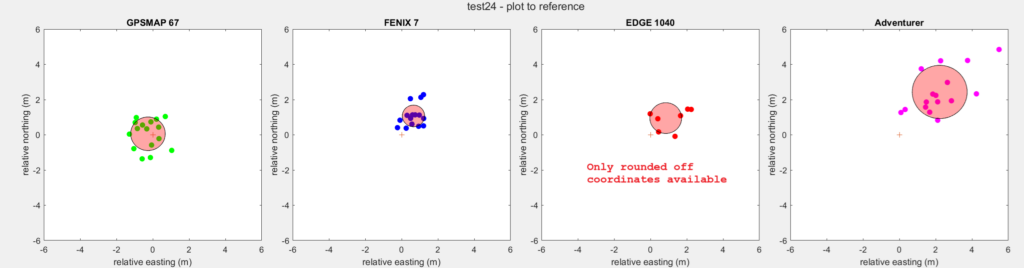
| GPSMAP 67 | Fenix 7 | Edge 1040 | Adventurer | |
| Measurements | 16 | 16 | 16 | 16 |
| Measurement time | 20′ | 20′ | 20′ | 20′ |
| Average accuracy error (m) | 1.0 | 1.3 | 1.4 | 3.4 |
| Average precision error (m) | 1.0 | 0.6 | 0.9 | 1.5 |
The GPSMAP 67 average coordinate coincides with the actual location, within the precision of the device. The other devices still show a systematic error to north-east. Reason unclear. Maybe the presence of a large metal plate (north west of the reference) has something to do with it. Or the impossibility to approach the reference point from the north (it’s always from the west, east or south).
Waypoints are usually logged as [name, datetime, latitude, longitude, elevation] in a GPX or FIT file. We observed following:
* The Fenix 7 does not register the datetime as attribute in the FIT file. Instead it puts the datetime in the name of the waypoint, like ‘Feb 02 1117’, hence minute granularity. This makes it less easy to correlate on a per second basis to the track data
* The waypoint as registered by the Fenix 7 appears not to be the same as the trackpoint logged at the same time. (e.g. Waypoint: N 53.02207938, E 6.78849240 Trackpoint: N 53.02208341, E 6.78847304). Waypoints were used though.
* The Edge 1040 somehow rounds off the lat,lon. Quite some overlapping waypoints were found. Therefore we took the datetime from the waypoint and used the coordinate from the track for that datetime.
* The GPSMAP 67 writes the waypoint lat, lon with six decimals (~1 m) to a GPX file, which is to course. Therefore we took the datetime from the waypoint and used the coordinate from the track for that datetime in eight decimals (~1cm). One coordinate logged in the GPX file was entirely wrong with respect to the track (N 53.02190800, E 6.78902800 instead of N 53.02206505, E 6.78848854, a difference of 41 m) !
We observe following:
* In three measurements on different days we observed a systematic error in all devices in which the indicated coordinate appears to the north east to the actual coordinate. In two out of three measurements this deviation is not visible in the GPSMAP 67. The error apparently changes over time. This was also seen with the stationary measurement: a 12 hours measurement shows a less precise measurement than a 2 hours measurement.
* The GPSMAP 67 shows the best accuracy.
* The Garmins appear to have comparable precision with an average error of 0.8-0.9 m. For the GPSMAP 67 this value is comparable to the value measured during the 2h stationary setup.
* The TomTom performs less regarding accuracy and precision as we might expect because of the older technology it uses.
Comparison under normal use
A number of cycling trips were executed with the Fenix 7 (left wrist), Edge 1040 (steering rod) and GPSMAP 67 (breast pocket).
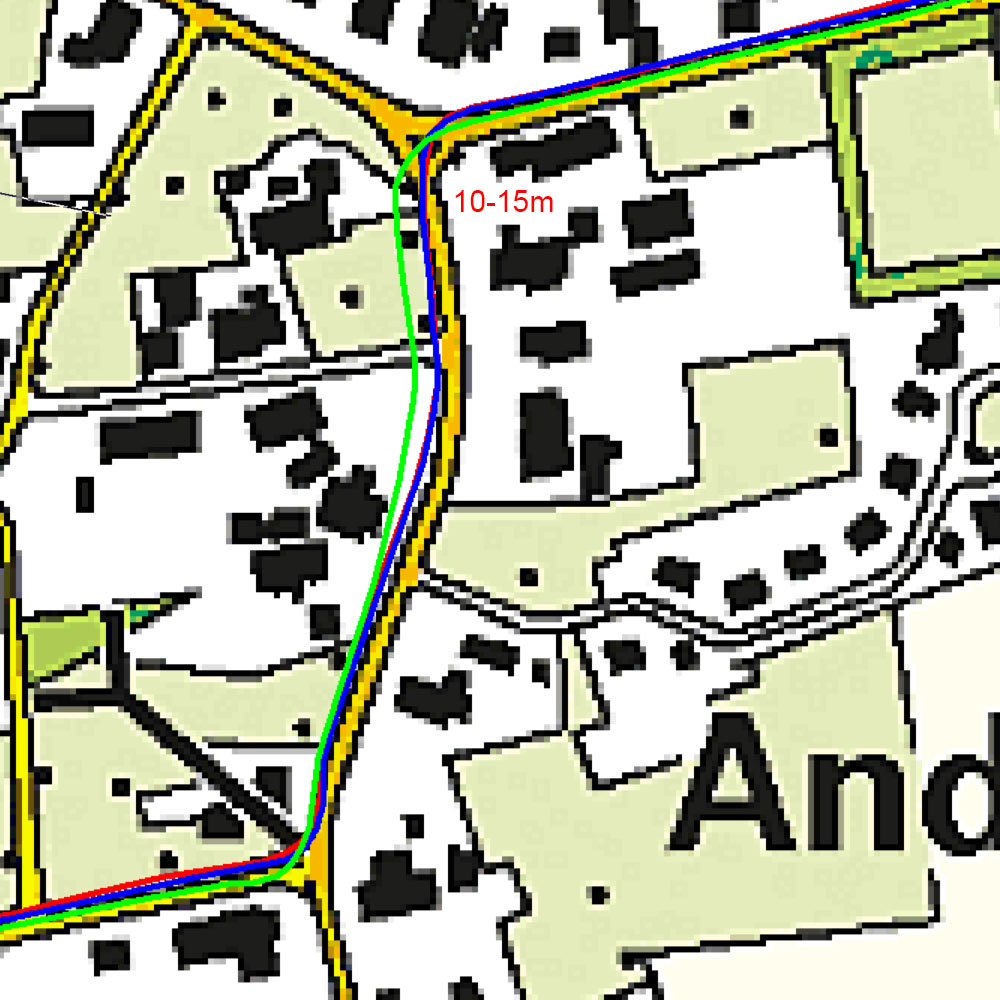
A remarkable observation is that the track logged by the Fenix 7 and Edge 1040 coincide most of the time. The GPSMAP 67 occasionally deviates. Sometimes overshooting, sometimes smoothing. We’ve seen this in the 4 Mile test. However, during the bike trips it has been observed, like the observation during an MTB trip we started this post with. Another typical ‘overshoot’ example is shown below.
Next example shows a typical ‘smoothing’ example.
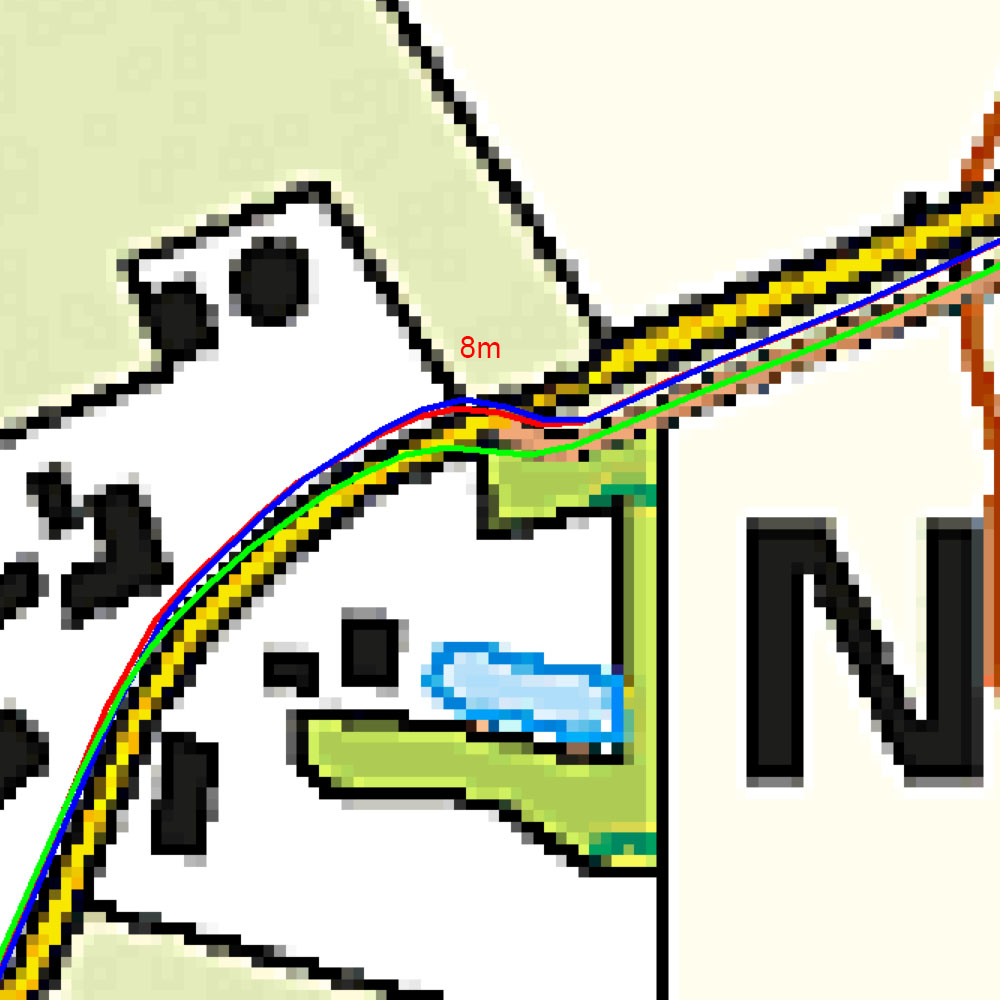
Based on normal use we observe the Fenix 7 and Edge 1040 to deliver tracks that show good correlation. Normally the GPSMAP correlates well, but occasionally it deviates shown overshoot or more smooting./
Of course, we cannot prove which device does the better logging, but it is 2 against 1.
Comparison in practice under harsh conditions (Update 12-06-2025)
To be honest, the main reason I bought the GPSMAP 67 is that I wanted the most accurate recording of the hikes during a upcoming vacation to Madeira. Madeira is very mountainous. I expected to get a more accurate recording with the GPSMAP 67 than with the Fenix 7 watch. So we did several hikes on which I took the GPSMAP 67 on my shoulder and the Fenix 7 on my wrist. Lots of hikes on Madeira are along steep mountain walls and are to and fro along the same route. This allows for a precision compare: we have for each device two recordings for the same track, which ideally should coincide.

To my surprise the GPSMAP 67 showed each hike larger deviations than the Fenix 7. Typical examples are shown in the next picture:
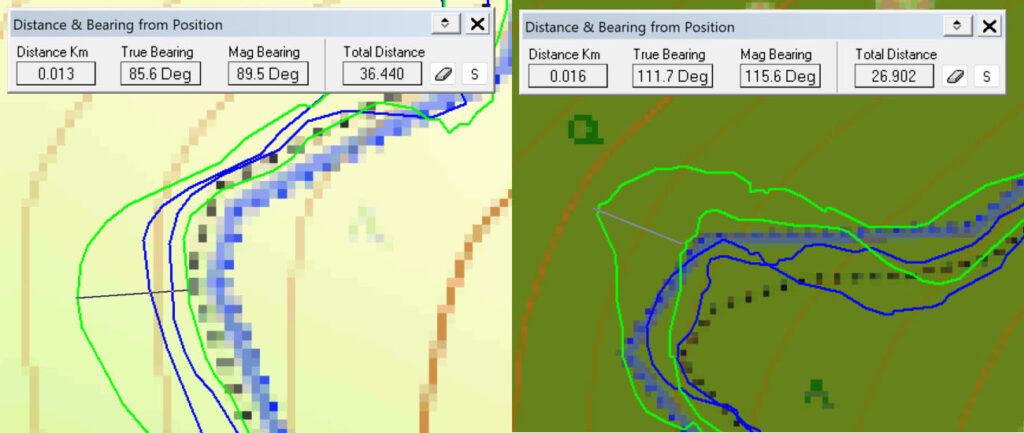
For a number of hikes I counted the deviations between the to and fro recordings that are larger than 10 m.
| Hike | Deviations >10 m Fenix 7 | Deviations > 10 m GPSMAP 67 |
| Levada da Ribeira da Janela | 3 | 8 |
| Levada do Risco, 25 fontes | 0 | 5 |
| Cural das Freiras | 0 | 4 (one deviation of 40 m!) |
| Levada do Caldeirão Verde (Very steep walls) | 4 | 7 |
For me this disqualifies the GPSMAP 67.
Conclusion
Precision
Several tests have executed to measure the precision of the four contestants under easy and medium GPS conditions. The GPSMAP 67 shows the highest precision, followed by the Edge 1040 and the Fenix 7. The least precise is the TomTom Adventurer.
However… Under harsh GPS conditions found in practice (mountainous area) the GPSMAP 67 shows serious deviations with respect to the Fenix 7.
The Garmins have the same Airoha GPS processor and support Multi-GNSS/Multi-band, so based on this we won’t expect too much of a difference. The GPSMAP 67 has the best antenna. It has been found it performs best with the antenna pointing upward. Due to this quad helix antenna the GPSMAP67 should be less susceptible to reflections and therefore perform better in harsh GPS conditions (mountains, urban jungle). However, we found the opposite. The Fenix 7 is expected to have the smallest antenna, because of its small form factor. However this device performs remarkable well in harsh conditions. The TomTom has an older Sirfstar V chip, which does not support Multi-GNSS/Multiband, so it is not surprising that it shows the least precision (which still is acceptable I believe).
Accuracy under ideal GPS conditions
Based on the waypoint experiment the GPSMAP 67 shows the best accuracy for logging tracks. Waypoint coordinates are logged with 6 decimals (~1m), which is sufficient for practical user.
All devices show good accuracy and precision in distance logging. In the 4 Mile experiment we found accuracies within 0.1%.
General remarks on the GPSMAP 67
The GPS location as recored by the GPSMAP 67 shows huge drift and deviations when left stationary under less ideal GPS conditions. Sometimes this leads to a residual error that is permanent and can only be recovered from by executing a power off-power on. From a GPS you might expect the basic functionality that it indicates a position which is within a few meters of your actual position, which the GPSMAP 67 occasionally does not. In spite of the good measurements (made directly after switching on the device), this makes the device unreliable. I reported Garmin and they indicate it is intended behaviour. So it is not expected that this issue will be resolved by Garmin.
Furthermore we showed some effects which suggest that also electronic compass and/or acceleration sensor signals are used for GPS positioning. Maybe both findings have a relation.
In normal use (cycling) we sometimes encounter situations in which the GPSMAP 67 track deviates from the other two, showing overshoot or more smoothing.
Because of this I am not going to use the GPSMAP 67. I obtained a secondhand GPSMAP 66sr (predecessor of the GPSMAP 67) and will post another blog on a comparison between both of them.
Bottomline
- Do not use the GPSMAP 67 because it is unreliable in less than ideal GPS conditions.
- For biking use the Edge 1040
- For all other activities the Fenix 7.

